Grating Solver Development Company
Deep Grating Example:
GSolver is numerically stable for very deep gratings. To illustrate this create a simple binary grating in Aluminum. (See the User's Manual for guidance.)
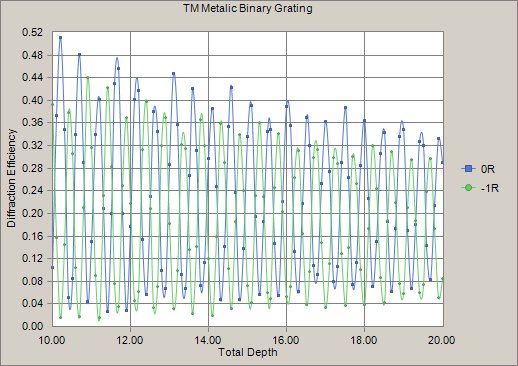
In this example I looked at the TE and TM polarization diffraction efficiency as a function grating (grove) depth. The aluminum substrate and 50% duty cycle aluminum grating had 800 lines/mm, 1 micron wavelength at 30 degrees incidence. 13 orders (total of 27) were retained.
The figure below shows the TE diffraction efficiency for a groove depth from 10 to 20 microns. This calculation could be extended to groove depths well beyond thousands of wavlengths without encountering numerical issues.
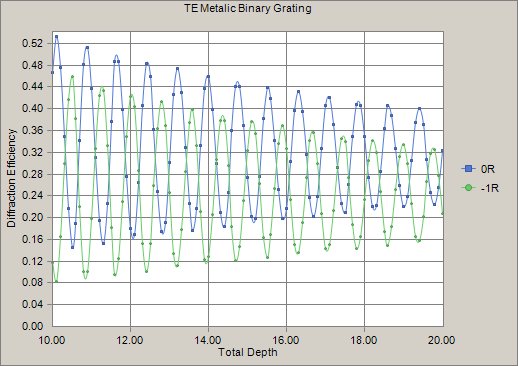
This next figure shows the same calculation for the TM mode.